As the release of Space Game v0.1.3 approaches, I thought I would discuss one of the more challenging obstacles that was blocking its release. I first noticed something was wrong when traveling to certain “corners” of the demo planet in the game. Performance would drop, and the simulation would attempt to request and render thousands of terrain nodes. Towards the spawn region — and most of the rest of the planet — I never noticed this performance hit. For a while, this seemed like a minor issue and I just left it on the backburner. Well, it turns out that the issue was a bit more sinister.
To give some background, the planet renderer originally used the naïve cube-to-sphere projection of simply normalizing the quadtree cube coordinates and scaling to the planet radius. This method can be seen in the image below. The red dots indicate vertices placed at equal intervals on the cube’s surface. These vertices are then “pushed” along their normals relative to the center point until they reach the sphere surface (marked with green dots). Notice the green dots are no longer at equal intervals on the sphere surface. This introduces a distortion with more vertex density towards the face edges.
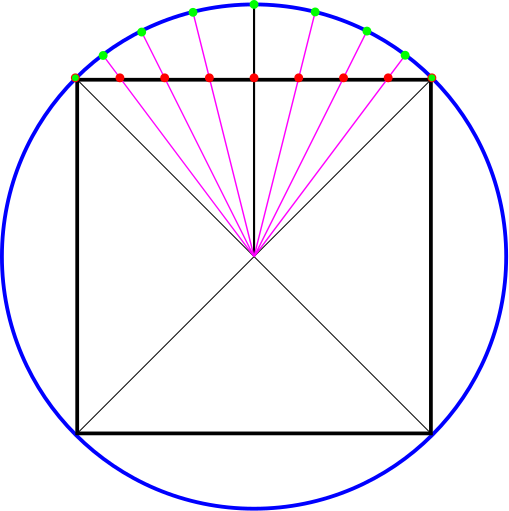
In the terrain renderer, each pair of dots constitutes a renderable tile. This means that as the player approaches the edges of the former cube faces, more terrain tiles would be required and performance would drop. To solve this, I implemented a projection scheme that would warp the position of the cube face coordinates such that when they were projected, they would create (nearly) equal area regions on the sphere surface. Terrain tile density would remain mostly constant and gameplay should stay smooth. The desired projection is shown below.
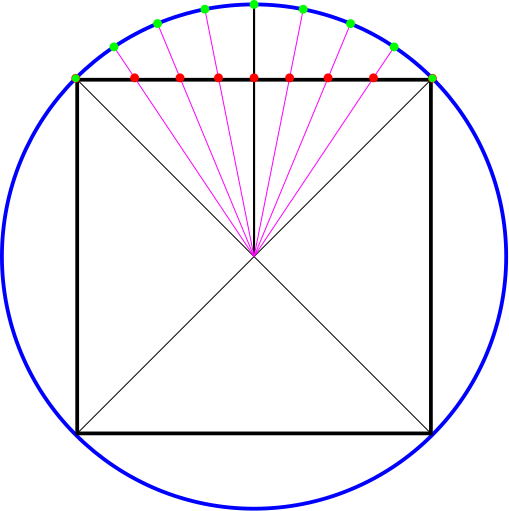
The cube face coordinates (red) are now warped towards the center of the face such that after the sphere projection they are at equal area intervals (green). As it turns out, this is a projection that is easy to compute an exact solution for in 2D, but difficult in 3D. My goal was to find a projection that minimized computation, but also provided an equal area solution to an acceptable margin of error.
After some research, I found a paper that went over several options for cube-to-sphere projection. The approach outlined in the paper that I found most desirable is the Odd Polynomial Univariate method. It had minimal area error, but was also very fast to compute. The method forms a 5th order polynomial with 3 coefficients that are optimized to minimize distortion.
![]()
This method further reduces the error beyond the similar tangent function, and it is a simple computation. So with this equation in place, I thought I had a sphere with nearly equal area distribution. I start up the game, head to a planet corner and… performance dropped to a slow crawl! After investigating for a few days, I found that the warping scheme was applied on my UV coordinates which were in the range [0, 1]. This caused the projection to push vertices into the (0, 0) corner of each face, resulting in extreme terrain tile counts in this region. After remapping the UVs to a [-1, 1] range, my performance was as I had predicted.
This was another one of those issues that seems simple in hindsight, but the processing of discovering the problem and tracing back its cause can be exceedingly difficult. The resulting mapping is now fairly uniform and has good performance all over the planet. Now that I’m done wasting time fiddling with renderer basics, I’m hoping I can get Space Game v0.1.3 out soon!